21 时间测量中随机误差的分布规律
初始化部分(不用阅读 直接跳过)
python
import pandas as pd
import numpy as np
import math
import matplotlib
import matplotlib.pyplot as plt
import os
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 用黑体显示中文
def toMarkdown(x,e): # 将数字转换为Markdown格式的科学计数法 精度格式为e
s=format(x,e)
l=s.split('e')
l[1]=str(int(l[1]))
if(l[1]== '0'):
return l[0]
return l[0]+'\\times10^{'+l[1]+'}'
accuracy=".2e"读取部分
请将你的数据放在同目录下的data.txt文件中,格式如下: 每一行一个数据(应该有200行),例如:
2.94
2.82
3.06
2.94
...
2.96
3.18
3.03输出为10个一行的表格
python
f=open('data.txt','r')
a=[]
for line in f:
a.append(float(line))
f.close()
n=len(a)
for i in range(n):
print(format(a[i],".2f"),end=' ')
if(i%10==9):
print()2.94 2.82 3.06 2.94 2.93 3.06 3.10 3.00 3.06 3.18
2.97 3.06 3.13 3.00 3.03 3.22 3.25 3.06 3.18 3.25
2.93 3.22 3.06 3.00 3.25 3.07 3.12 3.18 3.06 3.25
3.09 2.93 3.00 2.97 2.97 3.22 3.06 3.03 3.16 2.91
2.97 2.94 2.97 3.03 2.88 3.16 3.12 3.10 3.03 3.19
3.12 2.90 3.00 3.15 3.10 3.12 2.97 3.28 3.28 3.12
3.00 2.85 2.97 3.22 3.25 3.12 3.16 3.16 2.88 2.92
3.18 3.12 2.97 2.89 2.79 2.94 3.22 2.81 3.10 2.97
3.03 2.97 3.25 2.97 2.90 3.06 3.13 3.09 3.23 3.16
3.28 3.12 2.89 3.16 3.09 3.18 3.09 3.10 3.18 2.93
3.04 3.15 3.10 3.00 3.16 3.03 2.94 2.96 2.90 3.10
3.16 3.00 3.06 3.06 3.19 3.03 3.10 2.94 3.03 3.06
2.91 2.97 3.07 3.24 3.03 3.12 3.22 3.25 3.00 3.16
3.00 3.22 3.13 3.22 3.43 2.99 2.88 3.23 3.19 3.19
2.91 2.76 3.03 3.10 3.13 3.28 3.13 3.00 3.37 3.16
3.25 3.00 3.16 2.91 3.30 2.88 3.31 3.03 3.25 3.03
3.13 3.06 3.19 3.09 3.28 3.06 3.28 3.25 2.97 3.28
3.03 3.18 3.03 3.25 3.25 3.32 3.13 3.24 3.47 3.03
3.03 3.22 3.31 2.94 3.16 3.48 2.87 3.04 3.28 3.22
3.06 3.35 3.22 3.00 3.37 3.25 3.34 2.96 3.18 3.03
基础数据处理
计算平均值、标准差等统计量,并输出结果。
python
a_bar=round(np.mean(a),2)
a_max=round(max(a),2)
a_min=round(min(a),2)
a_std=round(np.std(a,ddof=1),4)
a_var=round(np.var(a,ddof=1),4)
R=round(a_max-a_min,2)
print("平均值: ",a_bar)
print("最大值: ",a_max)
print("最小值: ",a_min)
print("标准差: ",a_std)
print("方差: ",a_var)
print("极差: ",R)平均值: 3.09
最大值: 3.48
最小值: 2.76
标准差: 0.1352
方差: 0.0183
极差: 0.72
计算分段 统计频率
计算分段统计频率,输出分段区间、频数、频率、频率密度和概率密度函数值。
(Markdown)
$$ P(x,\bar x,\sigma) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\bar x)^2}{2\sigma^2}} $$调节下面的N值来改变分段数目,默认是14段。
python
def P(x,x_bar,sigma):
return 1/(math.sqrt(2*math.pi)*sigma)*math.exp(-(x-x_bar)**2/(2*(sigma**2)))
N=12
b=[0]*N
r=R/N# 每段的范围
b[0]=a_min+r/2
print("[",format(b[0]-r/2,'.2f'),",",format(b[0]+r/2,'.2f'),'],',end='')
for i in range(1,N):
b[i]=b[i-1]+r
print("(",format(b[i]-r/2,'.2f'),",",format(b[i]+r/2,'.2f'),'],',end='')
print(f"\n一共{N}段,每段长度为{r:.2f}")
cnt=[0]*N
for i in range(n):
for j in range(N):
if b[j]-r/2<a[i]<=b[j]+r/2:
cnt[j]+=1
if b[j]-r/2==a[i] and j==0:
cnt[j]+=1
print("普通格式:")
print("区间 频数 频率 频率密度 概率密度函数值")
for i in range(N):
print("(",format(b[i]-r/2,'.2f'),",",format(b[i]+r/2,'.2f'), #范围
'] ',cnt[i], #频数
' ',format(cnt[i]/n,'.2f'), #频率
' ',format(cnt[i]/(n*r),'.2f'), #频率密度
' ',format(P(b[i],a_bar,a_std),'.2f')) #概率密度函数值
print("Markdown格式:")
print("|区间$|$频数$|$频率$|$频率密度$|$概率密度函数值$|")
print("|:--:|:--:|:--:|:--:|:--:|")
for i in range(N):
print("|$(",format(b[i]-r/2,'.2f'),",",format(b[i]+r/2,'.2f'), #范围
']$|$',cnt[i], #频数
'$|$',format(cnt[i]/n,'.2f'), #频率
'$|$',format(cnt[i]/(n*r),'.2f'), #频率密度
'$|$',format(P(b[i],a_bar,a_std),'.2f'),'$|') #概率密度函数值[ 2.76 , 2.82 ],( 2.82 , 2.88 ],( 2.88 , 2.94 ],( 2.94 , 3.00 ],( 3.00 , 3.06 ],( 3.06 , 3.12 ],( 3.12 , 3.18 ],( 3.18 , 3.24 ],( 3.24 , 3.30 ],( 3.30 , 3.36 ],( 3.36 , 3.42 ],( 3.42 , 3.48 ],
一共12段,每段长度为0.06
普通格式:
区间 频数 频率 频率密度 概率密度函数值
( 2.76 , 2.82 ] 3 0.01 0.25 0.25
( 2.82 , 2.88 ] 2 0.01 0.17 0.61
( 2.88 , 2.94 ] 14 0.07 1.17 1.22
( 2.94 , 3.00 ] 16 0.08 1.33 1.99
( 3.00 , 3.06 ] 19 0.10 1.58 2.67
( 3.06 , 3.12 ] 16 0.08 1.33 2.95
( 3.12 , 3.18 ] 21 0.10 1.75 2.67
( 3.18 , 3.24 ] 18 0.09 1.50 1.99
( 3.24 , 3.30 ] 22 0.11 1.83 1.22
( 3.30 , 3.36 ] 5 0.03 0.42 0.61
( 3.36 , 3.42 ] 2 0.01 0.17 0.25
( 3.42 , 3.48 ] 3 0.01 0.25 0.09
Markdown格式:
|区间$|$频数$|$频率$|$频率密度$|$概率密度函数值$|
|:--:|:--:|:--:|:--:|:--:|
|$( 2.76 , 2.82 ]$|$ 3 $|$ 0.01 $|$ 0.25 $|$ 0.25 $|
|$( 2.82 , 2.88 ]$|$ 2 $|$ 0.01 $|$ 0.17 $|$ 0.61 $|
|$( 2.88 , 2.94 ]$|$ 14 $|$ 0.07 $|$ 1.17 $|$ 1.22 $|
|$( 2.94 , 3.00 ]$|$ 16 $|$ 0.08 $|$ 1.33 $|$ 1.99 $|
|$( 3.00 , 3.06 ]$|$ 19 $|$ 0.10 $|$ 1.58 $|$ 2.67 $|
|$( 3.06 , 3.12 ]$|$ 16 $|$ 0.08 $|$ 1.33 $|$ 2.95 $|
|$( 3.12 , 3.18 ]$|$ 21 $|$ 0.10 $|$ 1.75 $|$ 2.67 $|
|$( 3.18 , 3.24 ]$|$ 18 $|$ 0.09 $|$ 1.50 $|$ 1.99 $|
|$( 3.24 , 3.30 ]$|$ 22 $|$ 0.11 $|$ 1.83 $|$ 1.22 $|
|$( 3.30 , 3.36 ]$|$ 5 $|$ 0.03 $|$ 0.42 $|$ 0.61 $|
|$( 3.36 , 3.42 ]$|$ 2 $|$ 0.01 $|$ 0.17 $|$ 0.25 $|
|$( 3.42 , 3.48 ]$|$ 3 $|$ 0.01 $|$ 0.25 $|$ 0.09 $|
统计σ分布
输出结果 1σ、2σ、3σ的分布情况。 A类不确定度
python
sigm=[0]*4
for i in range(n):
for j in range(1,4):
if(abs(a[i]-a_bar)<=j*a_std):
sigm[j]+=1
print("σ分布:")
print("σ 频数 频率")
for i in range(1,4):
print(i,sigm[i],sigm[i]/n)
print('A类不确定度:',a_std*1.96/(n**0.5))σ分布:
σ 频数 频率
1 133 0.665
2 192 0.96
3 200 1.0
A类不确定度: 0.018737764016018555
画图
python
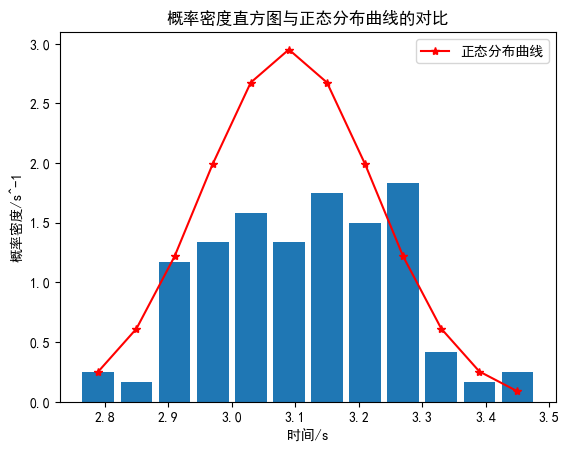
#折线图
p=[P(b[i],a_bar,a_std) for i in range(N)]
freq=[cnt[i]/(n*r) for i in range(N)]
plt.bar(b,freq,width=0.05)
plt.plot(b,p,color='red',label='正态分布曲线',marker='*')
plt.xlabel('时间/s')
plt.ylabel('概率密度/s^-1')
plt.title('概率密度直方图与正态分布曲线的对比')
plt.legend()
plt.show()
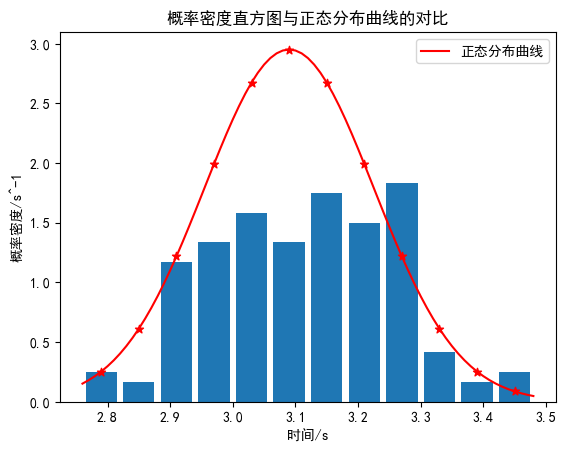
#曲线图
plt.bar(b,freq,width=0.05)
plt.scatter(b,p,color='red',marker='*')
x=np.arange(a_min,a_max,0.01)
y=[P(x,a_bar,a_std) for x in x]
plt.plot(x,y, color='red',label='正态分布曲线')
plt.xlabel('时间/s')
plt.ylabel('概率密度/s^-1')
plt.title('概率密度直方图与正态分布曲线的对比')
plt.legend()
plt.show()