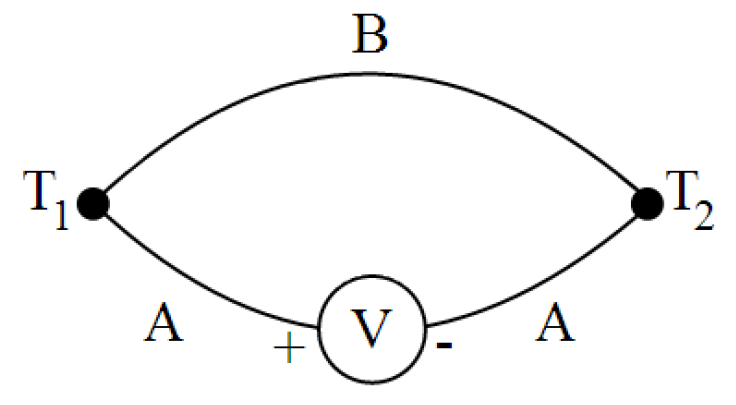
1821 年塞贝克(T. J. Seebeck)发现,当构成回路的两种不同金属的两个连接点温度不同时,回路中会有恒定电流产生,这表示两种金属的接触处由于温度差而产生了电动势(即温差电动势),该现象称为塞贝克效应,这种电路称为热电偶,如图1所示。

热电偶的温差电动势与两接头之间的温度关系比较复杂,可以用下式表示:
\[E=\int_{T_1}^{T_2} [S_B(T)-S_A(T)] dT\]式中,$E$为热电偶的电动势,$S_A(T)$和$S_B(T)$分别为两种金属在温度T时的热电势系数,$T_1$为热端的温度,$T_2$为冷端的温度。在较小的温差范围内,可近似地认为电动势$E$与温度差($T_2-T_1$)成正比,即:
\[E=C(T_2-T_1)\]式中,$C$为温差系数,单位为$mV/℃$,为相差$1℃$时的电动势,大小取决于组成热电偶材料的性质,有:
\[C=\frac{k}{e}ln(\frac{n_{0,A}}{n_{0,B}})\]式中,$k$为玻尔兹曼常数,$e$为自然对数的底数,$n_{0,A}$和$n_{0,B}$分别为两种金属单位体积内的自由电子数目。
对于热电偶,有以下俩个常见的定理:
如果在两种金属之间加入中间导体,当中间导体的两端温度相同时,引入中间导体对总电动势无影响。
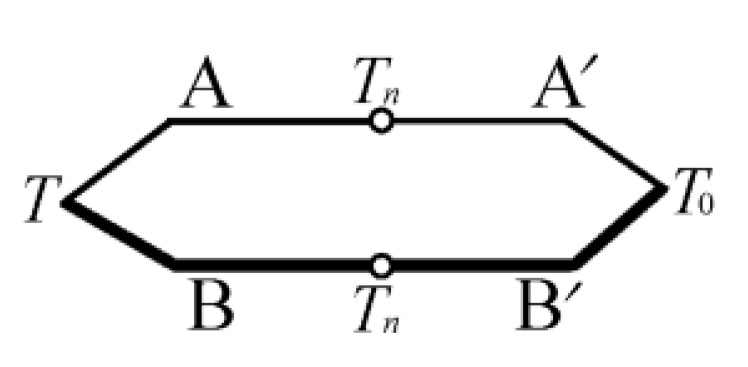
热电偶回路两接点(温度为$T_1$、$T_0$)间的热电势,等于热电偶在温度为$T_1$、$T_n$时的热电势与在温度为$T_n$、$T_0$时的热电势的代数和,如图2所示。$T_n$称中间温度。
利用温差热电偶测量温度时必须进行定标,即用实验的方法测量热电偶温差电动势与测量端温度之间的关系曲线,定标方法有以下两种:
1.比较法
即用被校准热电偶与一个标准热电偶(或标准热电阻)去测同一个温度,测得一组数据,其中被校准热电偶测得的热电势即由标准热电偶(或标准热电阻)所测的热电势所校准,在被校准热电偶的适用范围内改变不同的温度,进行逐点校准,就可以得到被校准热电偶的一条校准曲线。这种定标方法设备简单,操作方便,但其准确程度受到标准热电偶(或标准热电阻)准确度的限制。
2.固定点法
纯金属在融化和凝固过程中,其融化和凝固温度不随环境温度改变而改变,从而利用这些纯物质的融化和凝固温度作为已知温度,测出热电偶在这些温度下对应的电动势,利用作图法或最小二乘法拟合实验曲线,求出温差系数$C$,从而得到热电势与温度关系曲线。这种定标方法准确度很高,已被定为国际温标复现、校标的基准。
本实验定标时使用快速变温控温实验仪温度($Pt100$)作为参照。
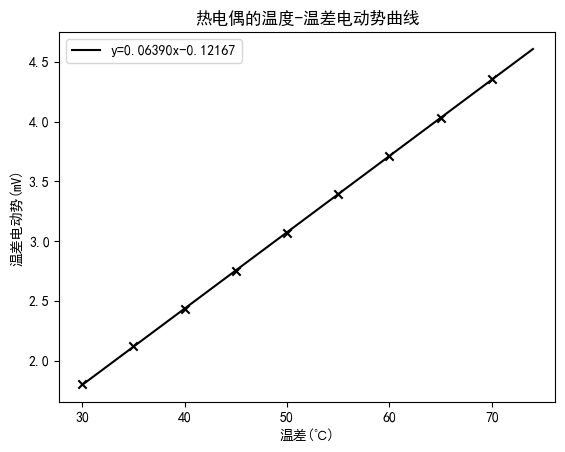
| $温差(℃)$ | $ 30 $ | $ 35 $ | $ 40 $ | $ 45 $ | $ 50 $ | $ 55 $ | $ 60 $ | $ 65 $ | $ 70 $ |
|---|---|---|---|---|---|---|---|---|---|
| $E(mV)$ | $ 1.80 $ | $ 2.12 $ | $ 2.43 $ | $ 2.75 $ | $ 3.07 $ | $ 3.39 $ | $ 3.71 $ | $ 4.03 $ | $ 4.36 $ |
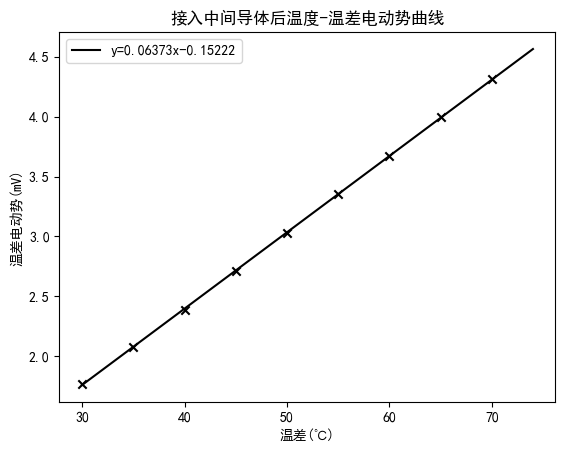
| $温差(℃)$ | $ 30 $ | $ 35 $ | $ 40 $ | $ 45 $ | $ 50 $ | $ 55 $ | $ 60 $ | $ 65 $ | $ 70 $ |
|---|---|---|---|---|---|---|---|---|---|
| $E(mV)$ | $ 1.77 $ | $ 2.08 $ | $ 2.39 $ | $ 2.71 $ | $ 3.03 $ | $ 3.35 $ | $ 3.67 $ | $ 4.00 $ | $ 4.31 $ |
根据测量数据,$E_{0-\text{手}}=2.18mV,E_{\text{手}-75}=2.19mV$,$E_{0-75}=4.36mV$,计算得 $Error=\frac{|(E_{0-\text{手}}+E_{\text{手}-75})-E_{0-75}|}{E_{0-75}}\times 100 \%=0.23\%$,可近似认为$E_{0-\text{手}}+E_{\text{手}-75}= E_{0-75}$,中间温度定律成立。
本实验使用快速变温控温实验仪($Pt100$)的温度为参照,测量了热电偶的温差电动势随着热端温度变化的特性,并通过回归拟合得到了其温差系数$C_1=63.90 \mu V/℃$,$C_2=63.73 \mu V/℃$,得出接入中间导体前后的温差系数$C_1≈C_2$,验证了中间导体定律;通过测得 $E_{0-\text{手}}=2.18mV; E_{\text{手}-75}=2.19mV; E_{0-75}=4.36mV$ ,故而 $E_{0-\text{手}} +E_{\text{手}-75} \approx E_{0-75}$ ,验证中间温度定律。实验结果表明,热电偶的温差电动势与温度差成正比,且中间导体定律和中间温度定律均成立。
在温度相关的实验中,常采用先升温后降温再取平均值的方法,该方法的优点是什么?该方法是否也适用于本实验?为什么?
优点如下:
该方法适用于热电偶特性的测量和中间导体定律的验证,不适用于中间温度定理的验证。
前两种实验是观察随着温度变化带来的电动势的变化,分别升温和降温的过程中测量可以减小测量时因为各种因素带来的误差。中间温度定律的验证没有温度动态变化的要求,只需要测量特定温度下的电动势,不需要通过升温和降温两次测量来减小误差。